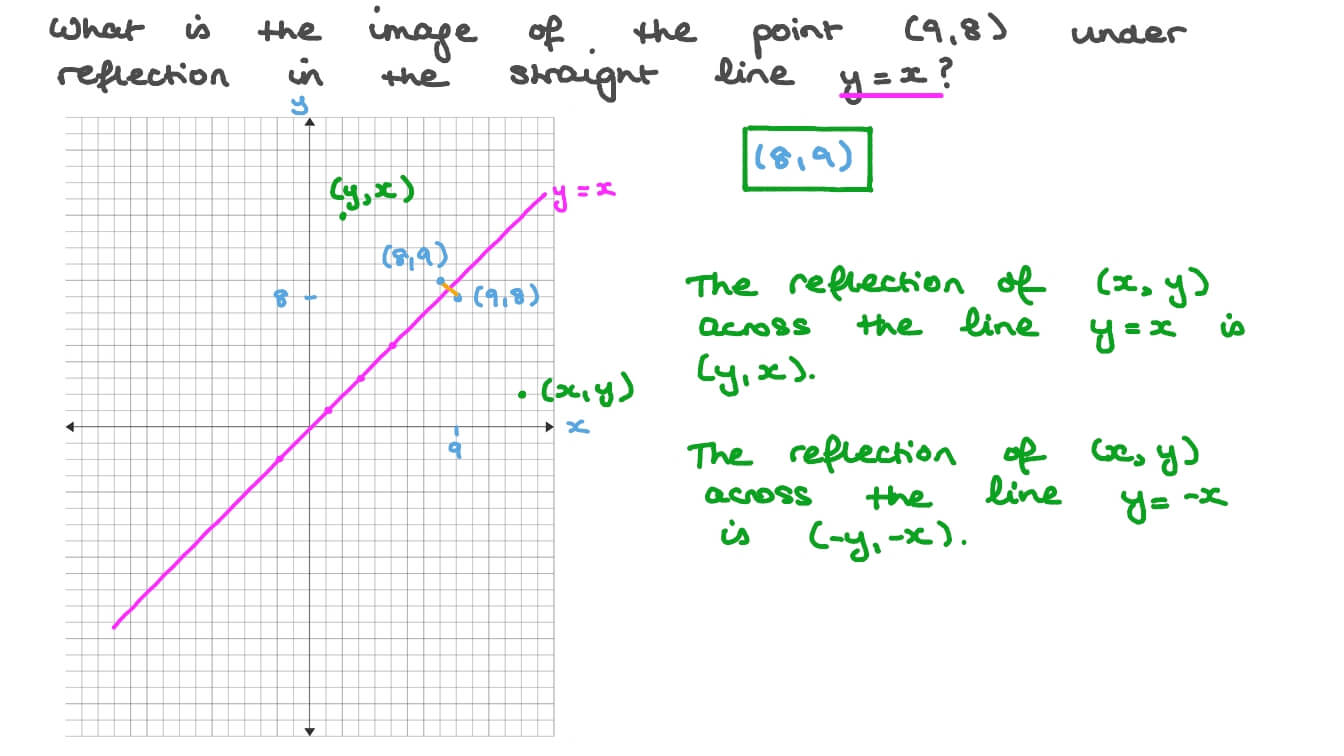
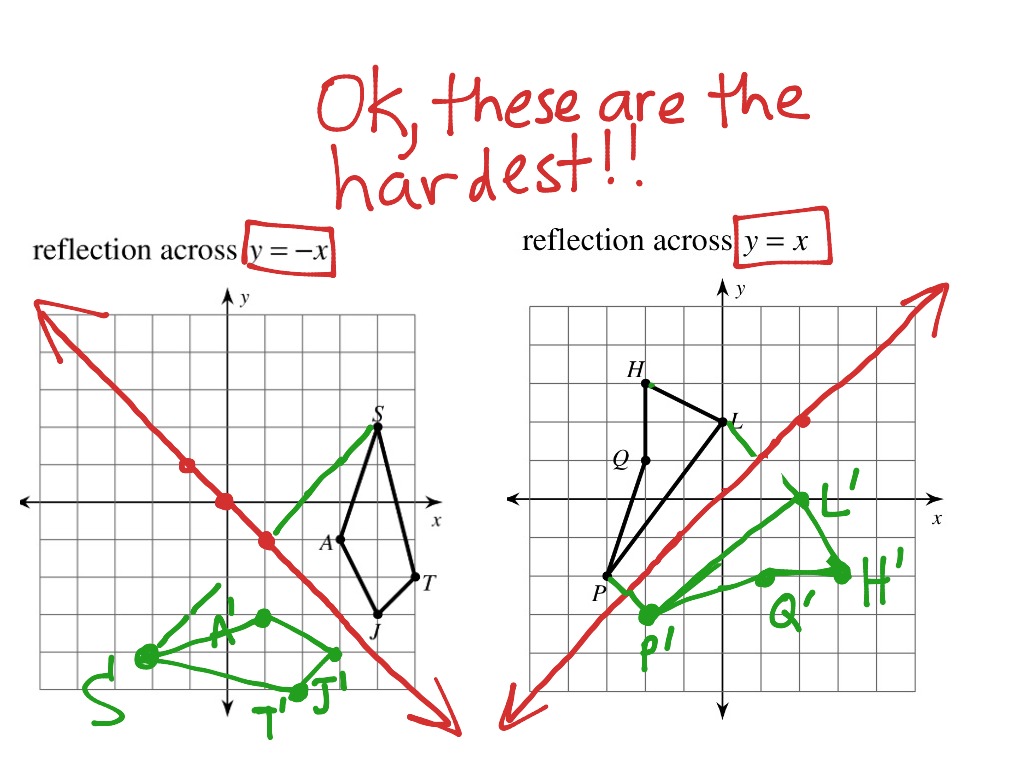
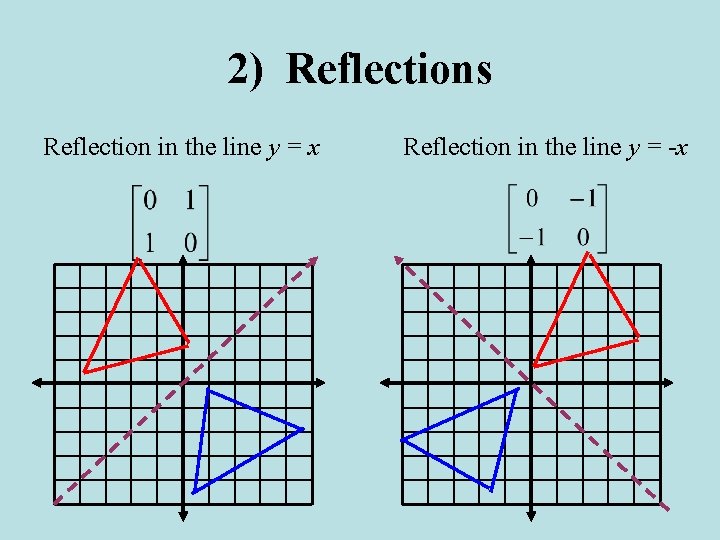
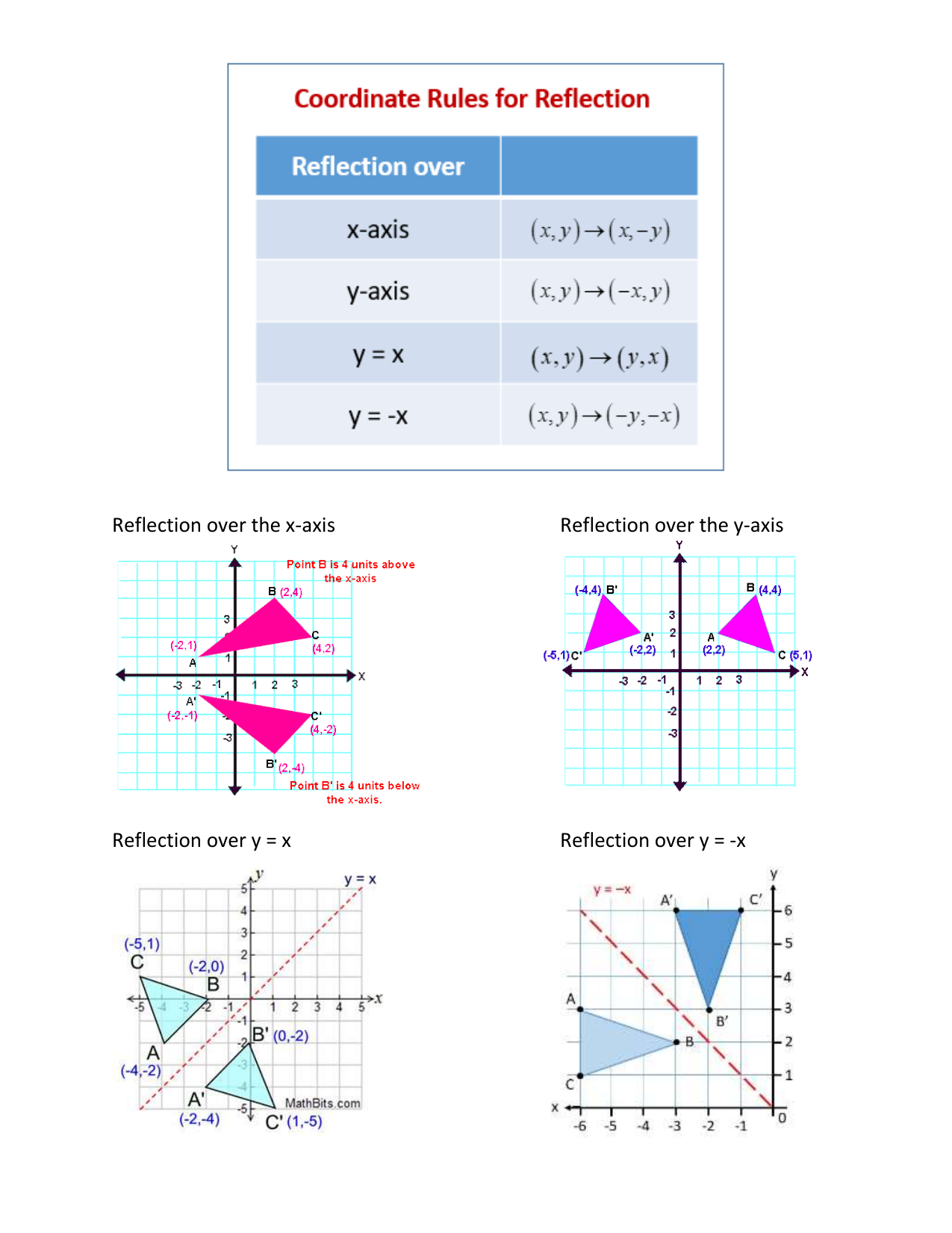
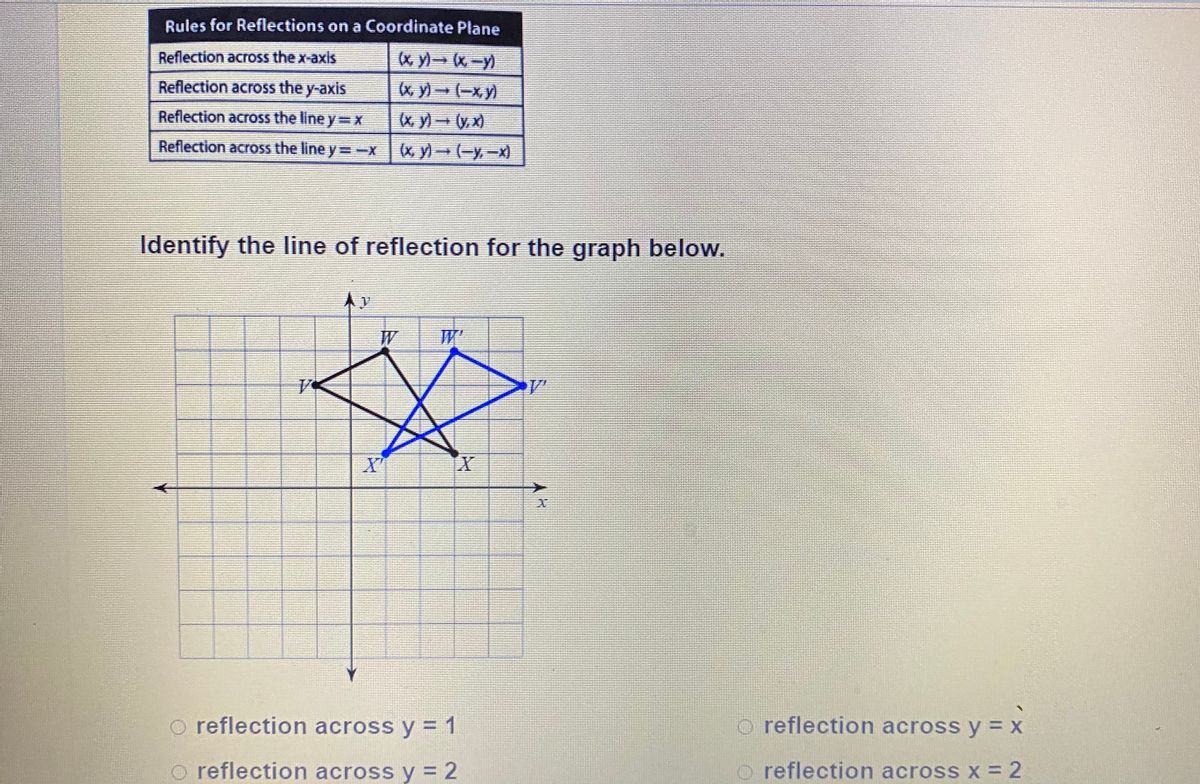
The reflection of the point (x, y) across the line y = x is (y, x) The reflection of the point (x, y) across the line y = – x is (y, x) Reflection in a Point A reflection point occurs when a figure is constructed around a single point known as the point of reflection or centre of the figureIf a reflection in the line y x occurs then the rule for this reflection is A reflection of a point over the line y x is shown This means all of the xcoordinates have been multiplied by 1 The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point but leave the x The Reflection is a mirror image of the original object In the Reflection process, the size of the object does not change We can represent Reflection by using four ways Reflection along Xaxis In this kind of Reflection, the value of X is positive, and the value of Y is negative

Transformations Of Graphs
Y=-x reflection matrix
Y=-x reflection matrix-The resulting orientation of the two figures are oppositeWe need an m x n matrix A to allow a linear transformation from Rn to Rm through Ax = b In the example, T R2 > R2 Hence, a 2 x 2 matrix is needed If we just used a 1 x 2 matrix A = 1 2, the transformation Ax would give us vectors in R1



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero
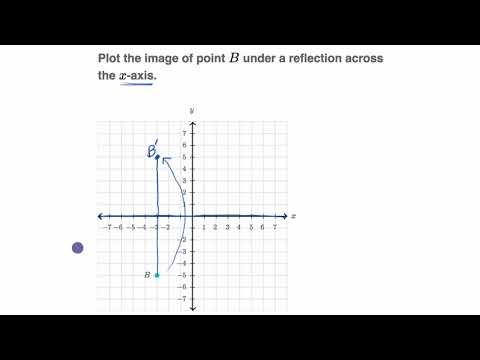
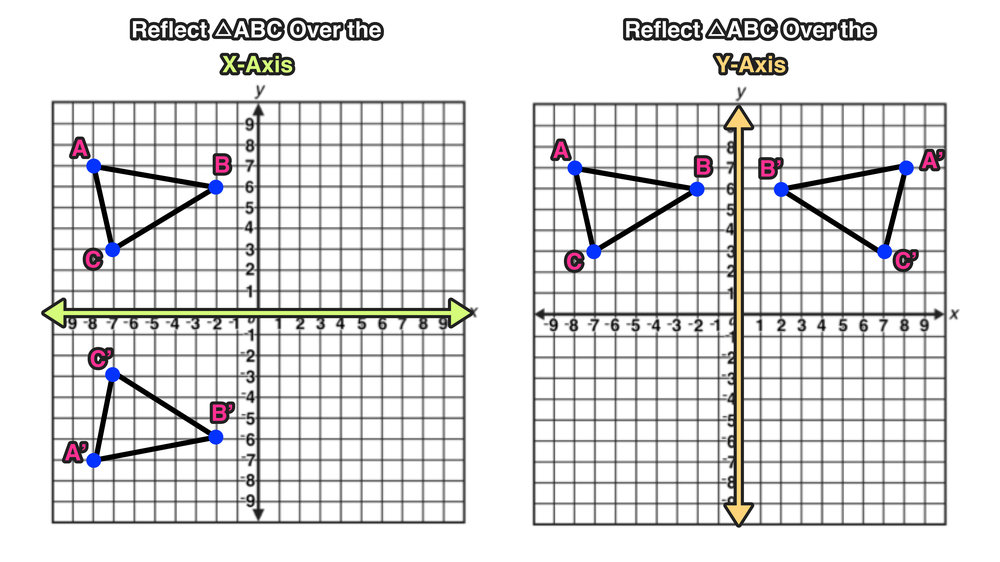
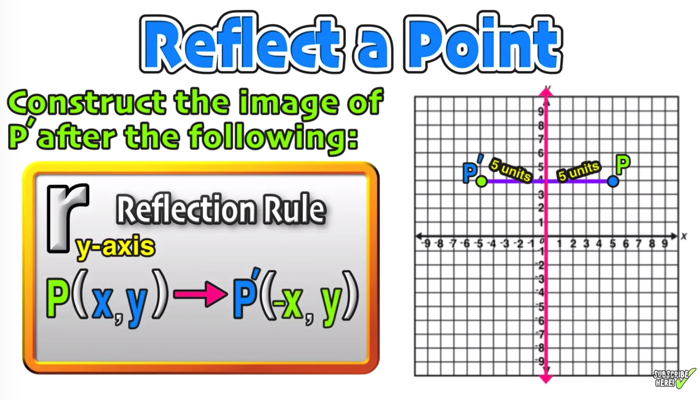
or y = x (2, 2) (4, 4) (5, 5) Just plotting a few of these coordinates will make sure that you always reflect in the correct mirror line The only other issue is to make sure that your reflection is at 90 degrees to the line, and it's the same distance both sides Other than that, you're good to go Here's some videos to helpTo perform a geometry reflection, a line of reflection is needed;The reflection of the point ( x,y) across the xaxis is the point ( x,y ) Reflect over the yaxis When you reflect a point across the y axis, the y coordinate remains the same, but the x coordinate is transformed into its opposite (its sign is changed) Notice that B is 5 horizontal units to the right of the y axis, and B' is 5 horizontal units to the left of the y axis
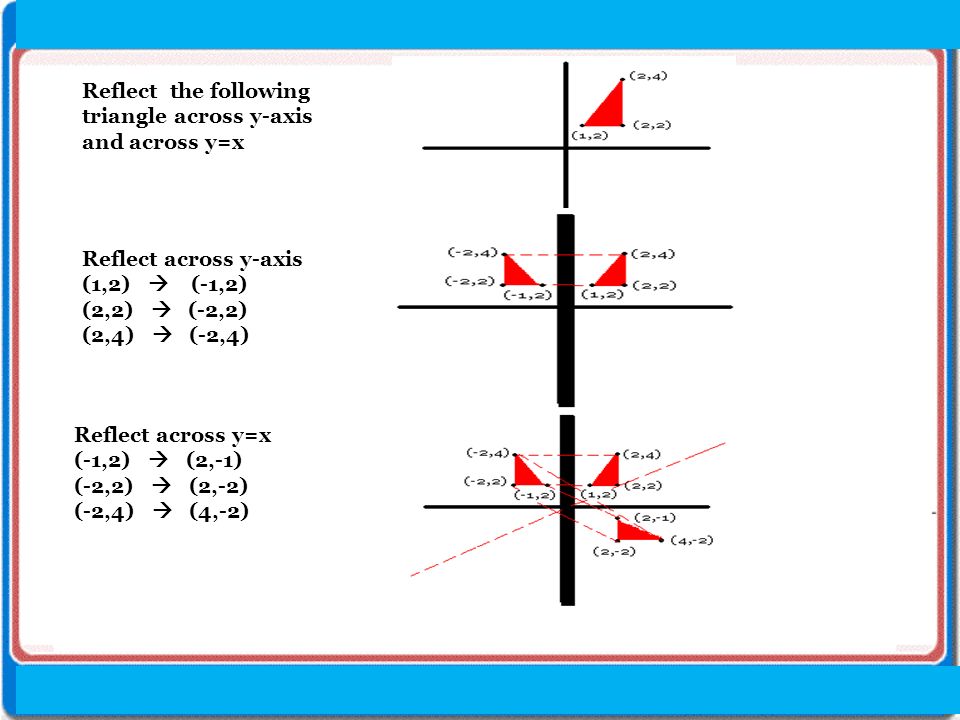
Reflection is a means of processing thoughts and feelings about an incident, or a difficult dayand gives us a chance to come to terms with our thoughts and feelings about it Reflection can be particularly useful in dealing with a difficult or challenging situation This type of reflection may take place when we have had time toY = x, the xcoordinate and ycoordinate change places and are negated (the signs are changed) the line y = x is the point (y, x) the line y = x is the point (y, x) Remember that each point of a reflected image is the same distance from the line of reflection asA reflection can be done through yaxis by folding or flipping an object over the y axis The original object is called the preimage, and the reflection is called the image If the preimage is labeled as ABC, then t he image is labeled using a prime symbol, such as A'B'C' An object and its reflection have the same shape and size, but the figures face in opposite directions
For a reflection in the line y=x $$\begin{bmatrix} 0 & 1\\ 1 & 0 \end{bmatrix}$$ Example We want to create a reflection of the vector in the xaxis $$\overrightarrow{A}=\begin{bmatrix} 1 & 3\\ 2 & 2 \end{bmatrix}$$ In order to create our reflection we must multiply it with correct reflection matrixShare this Click to share on Twitter (Opens in new window) Click to share on Facebook (Opens in new window)Swap places of x and y around True for any graph ln (x) is a reflection of e^x due to the same procedure 0 reply X start new discussion



Question Video Determining The Position Of A Point After Reflecting In A Given Straight Line Given The Point S Coordinates Nagwa



Reflecting Points Video Reflections Khan Academy
Reflection Over Y X In order to define or describe a reflection you need the equation of the line of reflection If a b is reflected on the line y x its image is the point b a Geometry Reflection A reflection is an isometry which means the original and image areY=x reflection Reflection Over the Line yx In this video you will learn how to do a reflection over the line y x ΔLMN with L M 15 and N 2 4 is reflected across the line y x For example if we are going to make reflection transformation of the point 23 about xUnlock StepbyStep reflect across y=2x Extended Keyboard Examples




Inverse Function Reflection In Y Axis Mathematics Stack Exchange



Math Alive Geometry 1
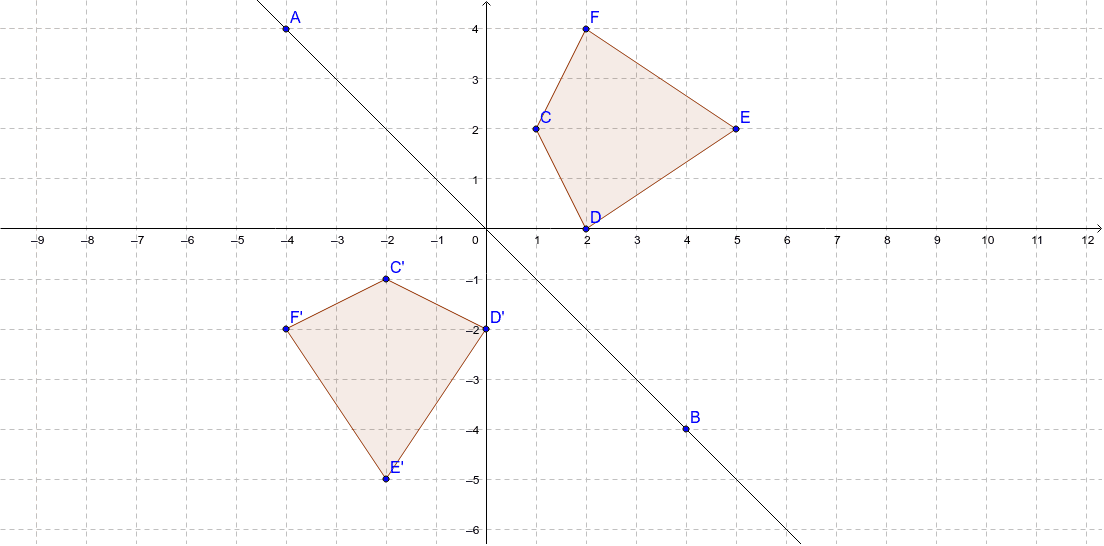
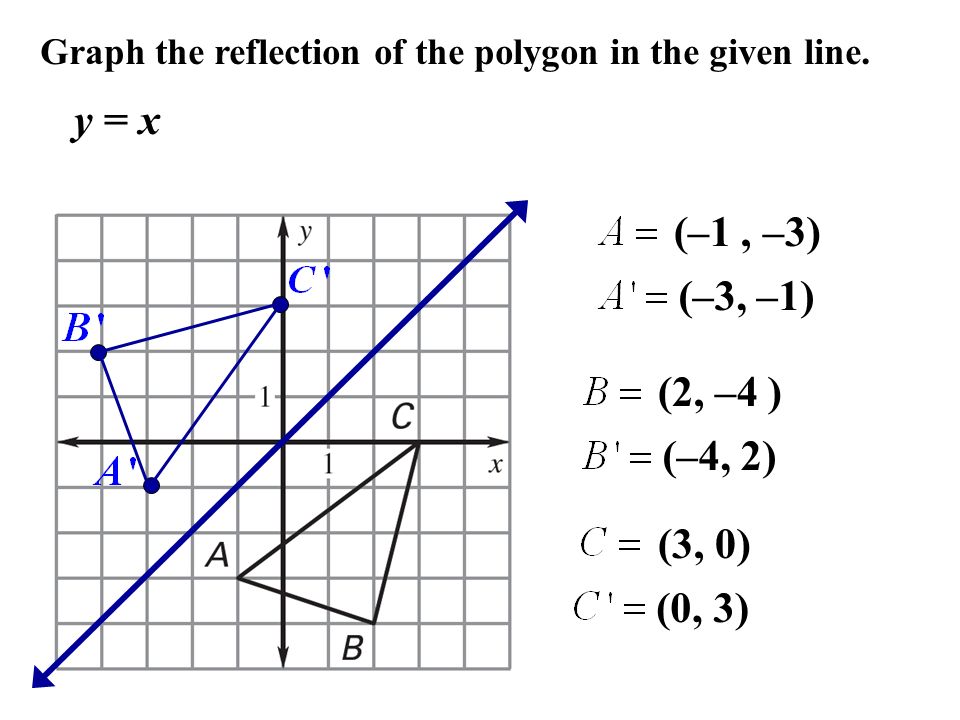
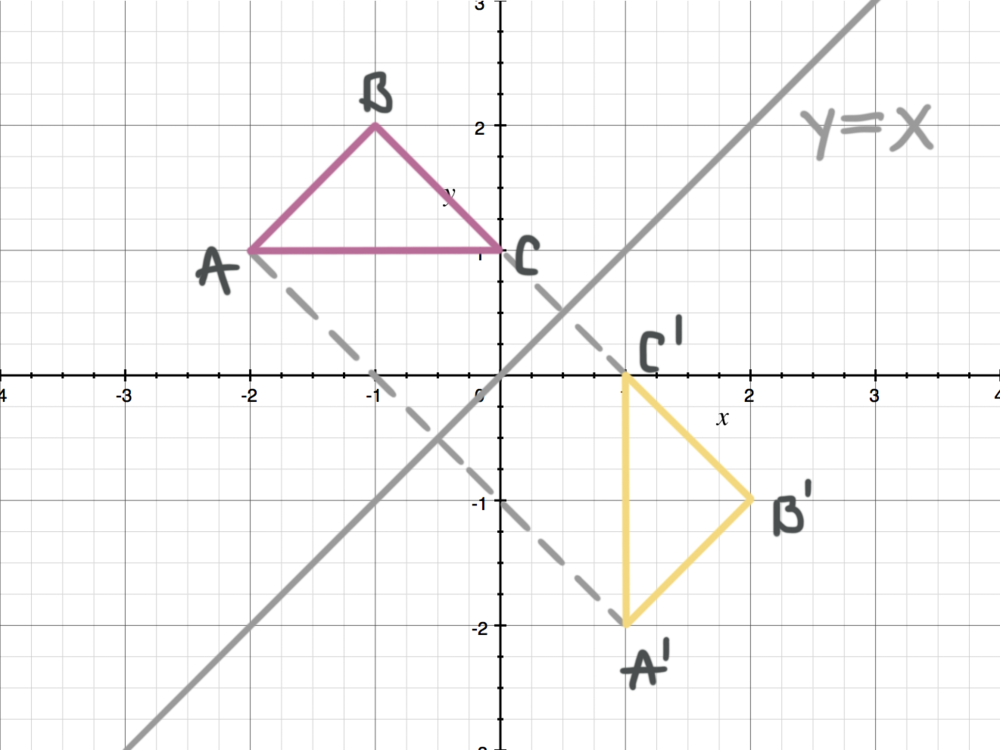
This is a KS3 lesson on reflecting a shape in the line y = x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendableGet the free "Reflection Calculator MyALevelMathsTutor" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Education widgets in WolframAlphaReflections across the line y = x A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC




Which Graph Shows A Reflection Across The Line Y X Brainly Com




Reflection Transformation Matrix
Horizontal and vertical reflections 5 Alternative versions feel free to create and share an alternate version that worked well for your class following the guidance here;This lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitterA Formula to Reflect a Point in y = −x Using Cartesian Coordinates In general, we write Cartesian coordinates as x is the xcoordinate y is the ycoordinate x and y can taken any number The reflected point has Cartesian coordinates The image below shows a general Cartesian coordinate being reflected in the line y = −x




Picture Of Reflection Across Y Axis Reflection Math Reflection Math




What Is A Line Of Reflection Printable Summary Virtual Nerd
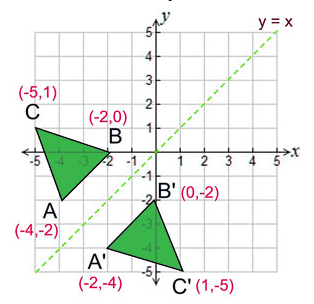
Reflection in the line y = x y = x is an equation of the line which makes an angle of 135° with the positive direction of X axis ∴ Slope of the line y = x is m 1 = tan 135° = 1 Let P (x, y) be any point in the plane Draw perpendicular PM from the point P to the line y = x and produce it to the point P' such that PM = MP'Revision notes on 'Transformations Reflection' for the Edexcel GCSE Maths exam Designed by the expert teachers at Save My Exams While reflecting about the line y=x, we get the reflected points by swapping the coordinates So, Option 3 is correct Now, the rule for reflecting a point about the line y= x is While reflecting about the line y= x, we get the reflected points by multiplying '1' with the swapped coordinates So, Option 2 is correct




Lesson On Line Of Reflection Y X



Compositions Of Reflections In Math Interactive Demonstration On How To Perform A Composition
If you reflect a point in the line y=x, your coordinates will simply swap place This is the simple observation you need to make before generalising it This is why in an equation thats all you need to do;More A point and its reflection over the line x=1 have two properties their ycoordinates are equal, and the average of their xcoordinates is 1 (so the sum of their xcoordinates is 1*2=2) So (2,3) reflected over the line x=1 gives (22,3) = (4,3) Comment on Ian Pulizzotto's post "A point and its reflection over the line x=1 haveY=x reflection The rule for a reflection over the y axis is x y x y Common Reflections About the Origin A reflection of a point over the y axis is shown First of all the object is rotated at 45 Example 1 – reflection a linear function across the line y x The last step is the rotation of yx back to its original position that is




Ppt Reflect Over Y X Powerpoint Presentation Free Download Id



Reflection Definition Reflection In The Coordinate Plane
Reflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3) Reflections Practice Questions – Corbettmaths Menu Skip to content Welcome Videos and Worksheets Primary 5aday expand child menu 5aday GCSE 91 5aday Primary SHOW ANSWER In the most simple terms, the solution would be y=x because this line, which travels straight through the origin, touching points (1,1) and (2,2), is the only given line that passes through the center of the given reflection After drawing the line, you can see that points C and C', B and B', and A and A' are exactly opposite




Reflections Geometry Abroad



Reflection Over Y X Geogebra
Reflection in the line y = x A reflection of a point over the line y = x is shown The rule for a reflection in the line y = x is ( x , y ) → ( y , x )Reflection is an example of a transformation A transformation is a way of changing the size or position of a shape Every point in the image is the same distance from the mirror line as theThe resulting orientation of the two figures are opposite Corresponding parts of the figures are the same distance from the line of reflection Ordered pair rules reflect over the xaxis (x, y), yaxis (x, y), line y=x (y, x) How do you describe reflection in math?




Reflections Across Y X Geogebra



R E F L E C T I O N O V E R Y X Zonealarm Results
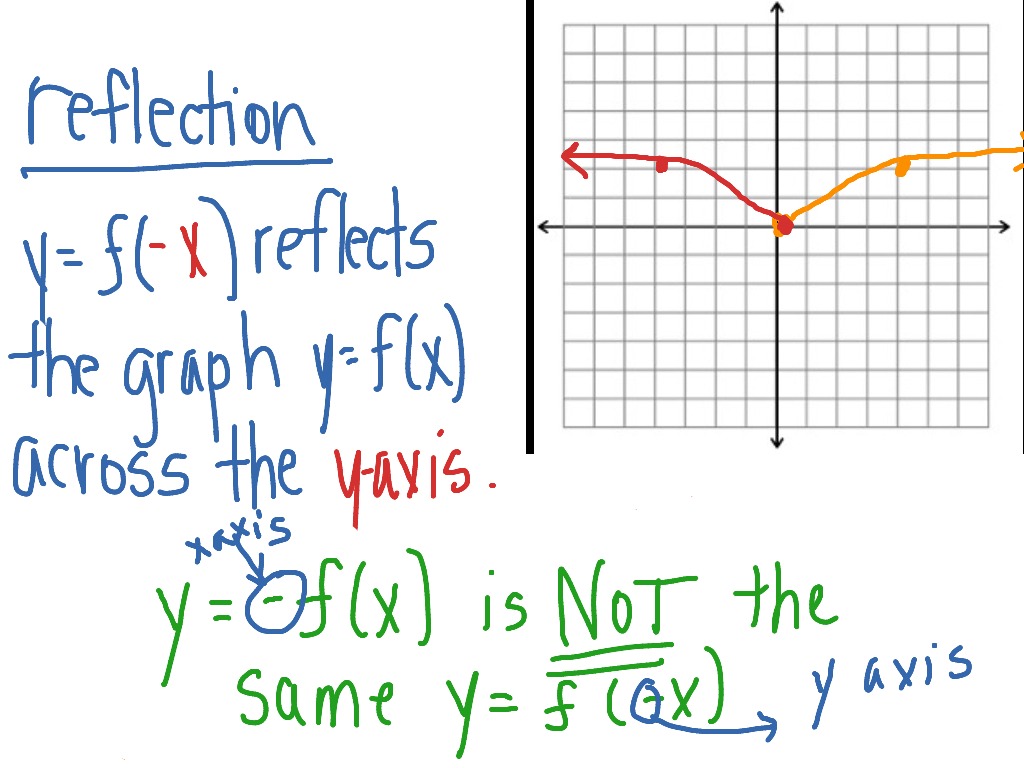
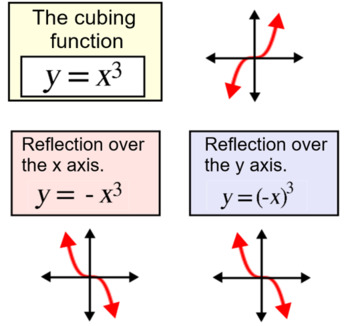
Reflection, Geometric Transformations Click and drag the blue dot to see it's reflection across the line y=x (the green dot) Pay attention to the coordinatesReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you wantReflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)



9 3 Perform Reflections Ppt Video Online Download



Search Q Coordinate Plane Tbm Isch
The rule for reflecting over the X axis is to negate the value of the ycoordinate of each point, but leave the xvalue the same For example, when point P with coordinates (5,4) is reflecting across the X axis and mapped onto point P', the coordinates of P' are (5,4)If (a, b) is reflected on the line y = x, its image is the point (b, a) Geometry Reflection A reflection is an isometry, which means the original and image are congruent, that can be described as a "flip" To perform a geometry reflection, a line of reflection is needed; Y=x reflection rule A 33 B 21 and C 62 would turn into A 33 B 12 and C 26 Reflection Over Y X In order to define or describe a reflection you need the equation of the line of reflection For triangle ABC with coordinate points A 33 B 21 and C 62 apply a reflection over the line yx Reflection Over y 2 With Rule by Lance Powell on




Reflecting Shapes Video Reflections Khan Academy



Reflection Over The X And Y Axis The Complete Guide Mashup Math
Reflecting Shapes in x and y Worksheet for students to use to reflect shapes in the x and y axes Also reflecting in the line y=x (diagonal line bottom left to top right) Report this resource to let us know if it violates our terms and conditionsA reflection of the point across the yaxis a reflection of the point across the line y = x a reflection of the point across the line y = x Click card to see definition 👆 Tap card to see definition 👆 B A reflection of the point across the yaxis Click again to see term 👆 Tap again to see term 👆Draw the triangle which has corners at the points with coordinates (1, 4), (1, 7) and (3, 5) Reflect this shape in the line y = x and state the coordinates of the corners of the reflected shape Reflect the original triangle in the line y = x and state the coordinates of the corners of the reflected shape
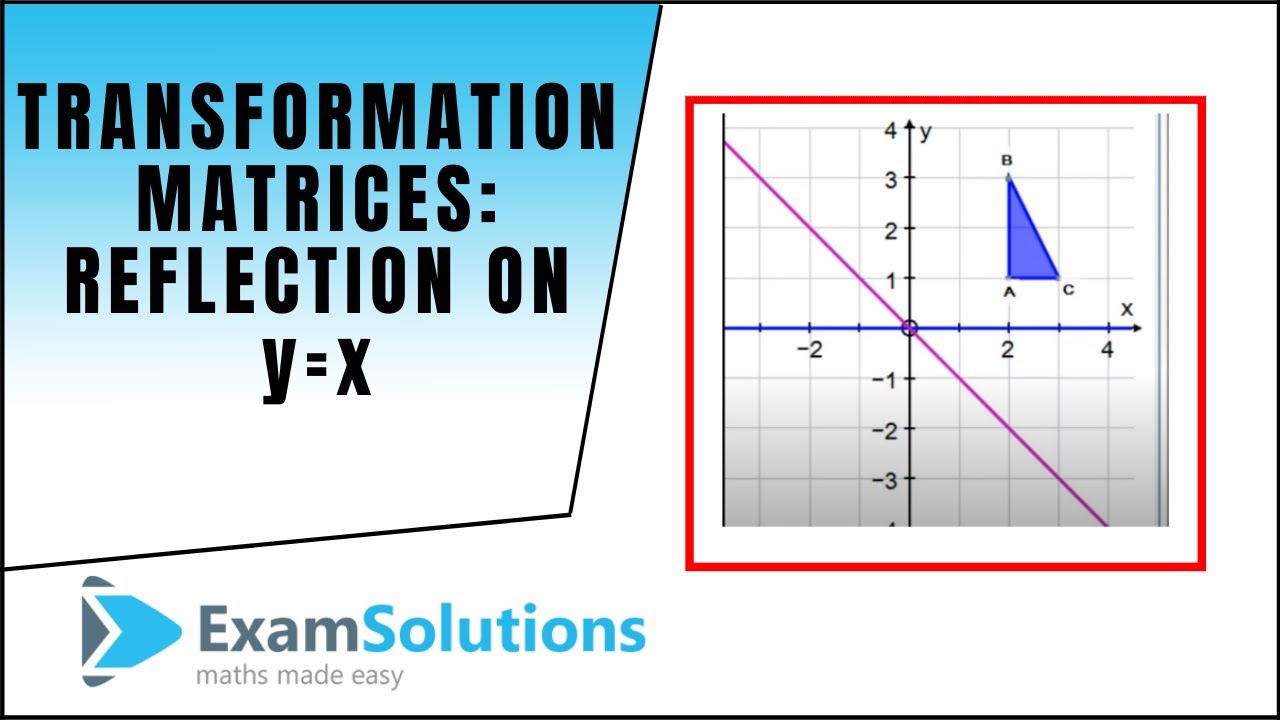



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube




Ixl Reflections Graph The Image Geometry Practice
Reflection When light from an object is reflected by a surface, it changes direction It bounces off the surface at the same angle as it hits it Smooth, shiny surfaces such as mirrors and




Reflection Transformation Matrix



Point 4 3 Is Reflected Over The Line Y X What Are The Coordinates Of The Reflection Mathskey Com




Common Reflections Key Stage 3




Graph The Image Of The Polygon After A Reflection In Chegg Com




Reflection Over The Line Y X Geogebra



Solved Graph A Triangle Label It Lmn And Reflect It Over The Line Y X To Create Triangle L M N Describe The Transformation Using Words Draw Course Hero




Reflection In The Line Y X Transformation Matrix Youtube




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com




Transformations Of Graphs




Algebraic Representations Of Reflections




Reflection Rules How To W 25 Step By Step Examples




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Reflection Over The Line Y X Math Showme
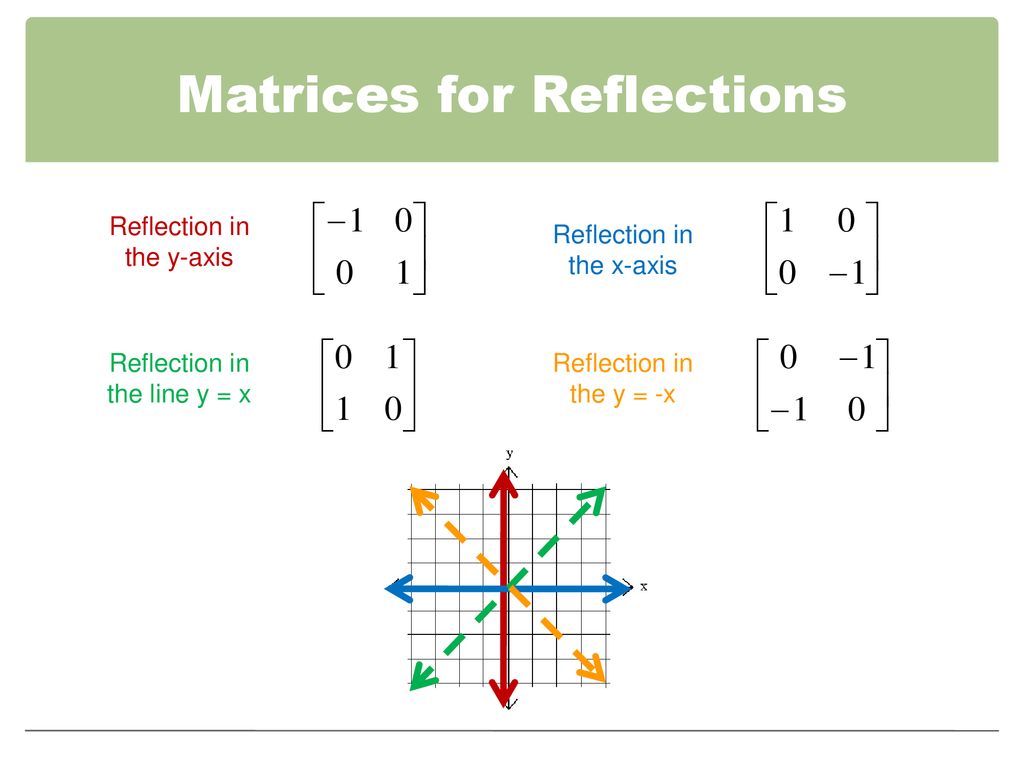



4 4 Geometric Transformations With Matrices Ppt Download




Geometry Transformations




Reflection Over The Y X Line Youtube




A Translation X Y X 5 Y Reflection Across Y Axis B Translation X Y X Y 5 Brainly Com




Reflection Transformation Matrix




Reflections Ck 12 Foundation




How To Find A Reflection Image



Search Q Translation Math Tbm Isch




Reflection Rules How To W 25 Step By Step Examples




Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Rules For Reflections Ck 12 Foundation




Reflection In Geometry Examples Solutions Videos Worksheets Games Activities
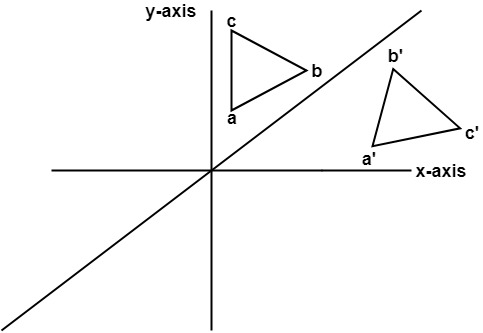



Computer Graphics Reflection Javatpoint
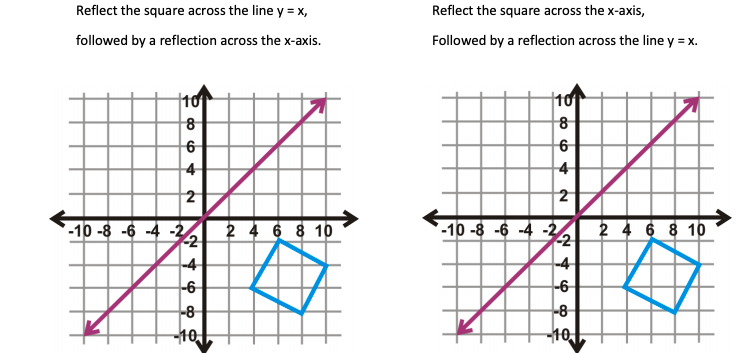



Reflect The Square Across The Line Y X Followed By Chegg Com



Reflections Math Analysis Functions




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor




Reflections Of Trig Graphs Examsolutions



1




Reflection Mathbitsnotebook A1 Ccss Math



Reflection Of A Point In A Line Assignment Point



Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf



4 4 Transformations With Matrices 2 Reflections And




More Reflections Easing The Hurry Syndrome




Reflection Mathbitsnotebook A1 Ccss Math



Reflections 30 Reflect Across Y X X Y Y X Reflect Across X Axis X Y X Y Reflect Across Y Axis X Y X Y Reflect Across Y X Reflect Across Ppt Download



Reflection Across The Y Axis Math Functions Showme




D Reflection Across Y X Brainly Com



1




Reflection Mathbitsnotebook A1 Ccss Math




A Line Segment Goes From 1 2 To 4 1 The Line Segment Is Reflected Across X 1 Reflected Across Y 3 And Then Dilated About 2 2 By A Factor



Biomath Transformation Of Graphs



How To Prove Say That Point X Y Becomes Y X On A Reflection On The Line Y X Using Only Geometry Quora
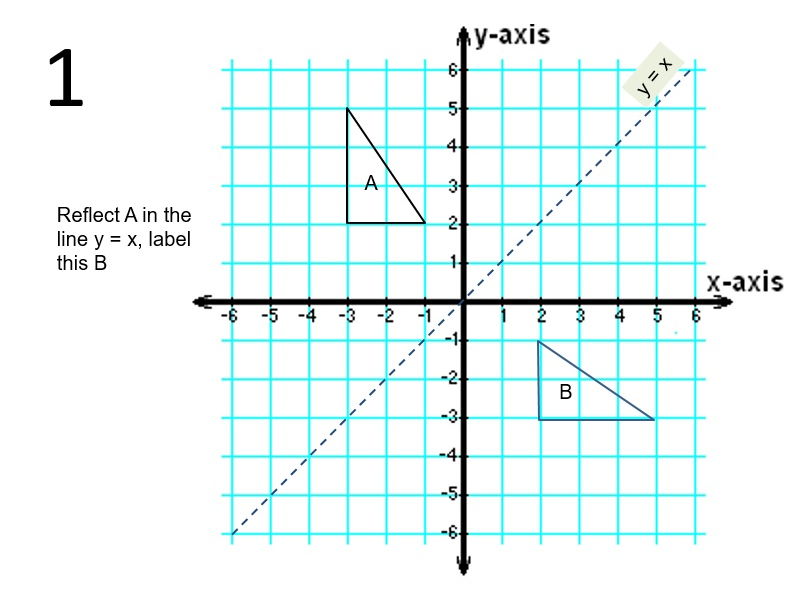



Diagonal Reflections In The Line Y X Teaching Resources
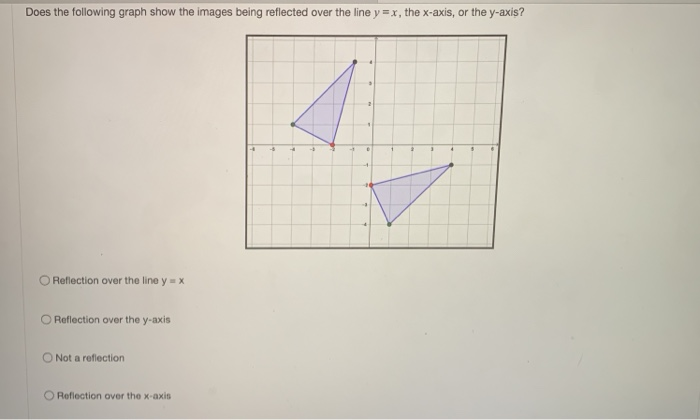



Does The Following Graph Show The Images Being Chegg Com




Reflection Rules How To W 25 Step By Step Examples



Assignment 2 Transforming Parabolas




Reflection Over Y X Math Geometry Showme




Line Of Reflection Y 0 Novocom Top
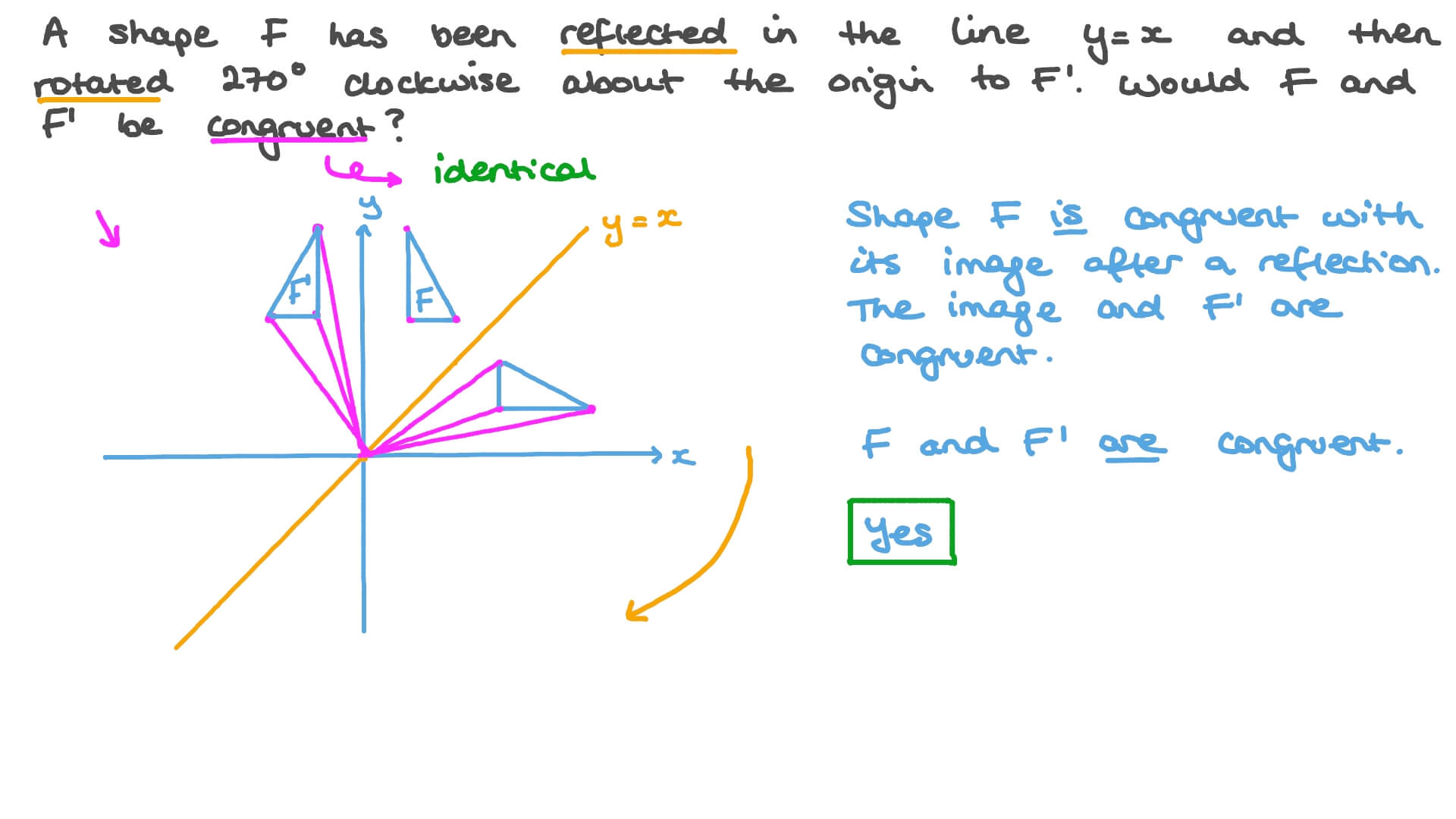



Question Video Understanding The Effects Of Reflection And Rotation On A Shape Nagwa
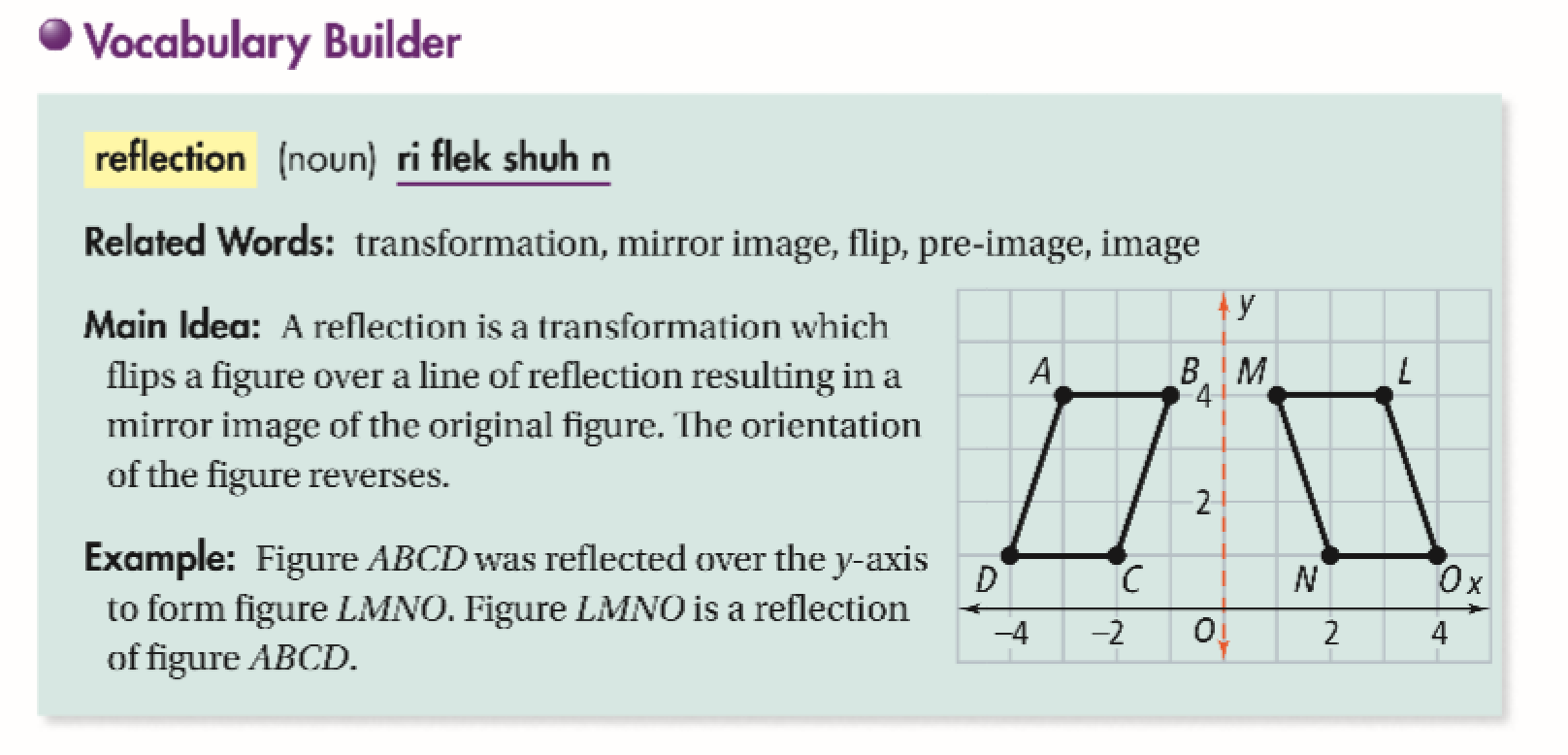



Reflections Across A Line Other Than Axis Or Y X Power Jasmin Library Formative



Reflection Rules Toolkit




Reflecting Functions Examples Video Khan Academy




What Are The Coordinates Of Point A 4 1 After It Has Been Reflected Over The Y Axis Socratic




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




Transformation Reflection Over The Line Y X Youtube




How To Find A Reflection Image




Learn About Reflection Over The Line Y X Caddell Prep Online




Geometry Reflection Across Y X Youtube




Picture Of Reflection In The Line Y X Reflection Math Math Reflection




Reflection Over Y 2 With Rule Educreations




Reflection Over A Line Expii
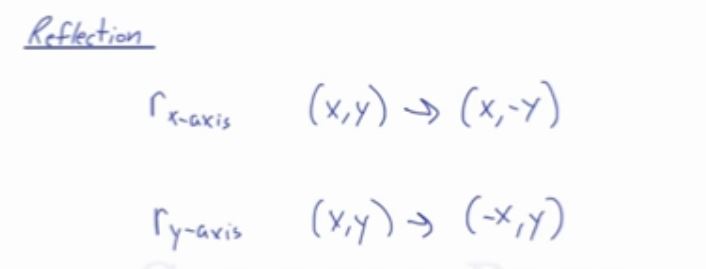



Learn About Reflection Over An Axis Over X Axis Or Y Axis



Answered Rules For Reflections On A Coordinate Bartleby




Coordinate Geometry Reflections On A Coordinate Plane Magoosh Math



Geogebra Project Rotations And Reflections Math At Dis




Reflections




Reflection In The Line Y X Geogebra




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




Translation With Geogebra Figure 2 Reflection Through Line Y X With Download Scientific Diagram




Reflection



Math Alive Geometry 1



What Does It Mean To Reflect Over The Y X Line Quora



Biomath Transformation Of Graphs




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3



Reflections Of Functions Over The X Y Axes Intro 2 Assignments For Smart



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Reflection Over The Line Y X Youtube



Solution After A Reflection In The Line Y X 2 4 Is The Image Of Point N What Is The Original Location Of Point N


